y se conocen como ecuaciones de Bernoulli.
a) Demostrar que si
![]() , entonces la substitución
, entonces la substitución
![]() reduce la ecuación de Bernoulli a una ecuación lineal.
reduce la ecuación de Bernoulli a una ecuación lineal.
b) Resolver las siguientes ecuaciones aplicando la substitución
del apartado a):
i)
![]()
ii)
![]() . Esta ecuación aparece en la dinámica de poblaciones.
. Esta ecuación aparece en la dinámica de poblaciones.
iii)
![]() .
Esta ecuación aparece en el estudio de la estabilidad del flujo de
fluidos.
.
Esta ecuación aparece en el estudio de la estabilidad del flujo de
fluidos.
se conoce como ecuación de Riccatti. Conocida una solución particular
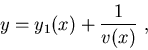
es posible obtener una solución general que contenga una constante arbitraria.
a) Demostrar que ![]() satisface la ecuación lineal de primer
orden
satisface la ecuación lineal de primer
orden
Mostrar que
b) Resolver las siguientes ecuaciones aplicando el método del apartado a):
i)
![]()
ii)
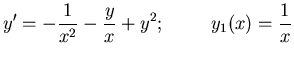
iii)
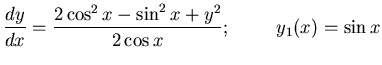
por dos métodos independientes:
a) Mediante el método de la ecuación de Riccatti. ¿Qué valor debe tomar la constante de integración para satisfacer la condición inicial?
[Ayuda: Una solución particular es la función
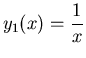 .]
.]
b) Mediante el método de cambio de variables. ¿Qué valor debe tomar la constante de integración para satisfacer la condición inicial?
[Ayuda: Considerar el cambio de variables ![]() .]
.]
c) Comentar los dos métodos. ¿Qué rango de aplicación tiene la solución del problema?
i) Derivar la ecuación respecto a
ii) Integrar la ecuación obtenida en i) para obtener
b) Resolver la ecuación diferencial
donde
c) Resolver la ecuación directamente y comparar las soluciones.
donde
a) Observar que esta ecuación es de Riccatti. Aplicar la
transformación sugerida en el problema 2. y hallar la ecuación
lineal que satisface ![]() .
.
[Ayuda: Notar que ![]() es una solución particular.]
es una solución particular.]
b) Calcular ![]() en el caso de que
en el caso de que ![]() , con
, con ![]() constante.
Expresar la solución en términos de la función error.
constante.
Expresar la solución en términos de la función error.
a) Considerar la familia de parábolas ![]() , donde
, donde ![]() es una
constante. Trazar la gráfica de dicha ecuación para varios valores
de
es una
constante. Trazar la gráfica de dicha ecuación para varios valores
de ![]() . Encontrar una expresión para la pendiente de la parábola que
pasa por un punto dado, de modo que esa expresión contenga las
coordenadas
. Encontrar una expresión para la pendiente de la parábola que
pasa por un punto dado, de modo que esa expresión contenga las
coordenadas ![]() del punto, pero no el parámetro
del punto, pero no el parámetro ![]() .
.
[Ayuda: Derivar la ecuación y eliminar ![]() .]
.]
b) Escribir la ecuación diferencial que satisfacen las trayectorias
ortogonales a ![]() .
.
[Ayuda: Las pendientes de curvas ortogonales son recíprocas negativas.]
c) Resolver la ecuación obtenida en b) y determinar las trayectorias ortogonales. Trazar varios elementos de esta familia de curvas.
| a) circunferencias:
|
b) elipses:
|
| c) hipérbolas: |
d) parábolas:
|
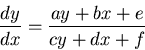
Demostrar que:
a) Si ![]() , entonces puede reducirse a una ecuación
homogénea mediante el cambio de variables:
, entonces puede reducirse a una ecuación
homogénea mediante el cambio de variables:
![]() ,
con
,
con ![]() y
y ![]() adecuados.
adecuados.
b) Si ![]() , entonces puede reducirse a una ecuación de
variables separadas mediante el cambio de variables:
, entonces puede reducirse a una ecuación de
variables separadas mediante el cambio de variables: ![]() .
.
Al resolver este problem es conveniente tomar el origen como el punto
superior ![]() y orientar los ejes de forma que el eje
y orientar los ejes de forma que el eje ![]() sea vertical
hacia abajo. El punto inferior tiene las coordenadas
sea vertical
hacia abajo. El punto inferior tiene las coordenadas ![]() .
Entonces, es posible demostrar que la curva de tiempo mínimo
queda definida por una función
.
Entonces, es posible demostrar que la curva de tiempo mínimo
queda definida por una función ![]() que satisface la ecuación
diferencial
que satisface la ecuación
diferencial
donde
a) Despejar ![]() de la ecuación. ¿Por qué es necesario elegir la
raiz cuadrada positiva?
de la ecuación. ¿Por qué es necesario elegir la
raiz cuadrada positiva?
b) Hacer el siguiente cambio de variables
![]() ,
y demostrar que la ecuación obtenida en el apartado a) toma entonces
la forma
,
y demostrar que la ecuación obtenida en el apartado a) toma entonces
la forma
c) Si se toma ![]() , demostrar que la solución de la
ecuación anterior que pasa por el origen se puede expresar por
, demostrar que la solución de la
ecuación anterior que pasa por el origen se puede expresar por
Estas ecuaciones son ecuaciones paramétricas de la solución de la primera ecuación, que pasa por
a) al cabo de ![]() segundos.
segundos.
b) cuando ha recorrido ![]() metros.
metros.
[Ayuda: Hay que tener en cuenta el efecto relativista que hace que
la masa del electrón varíe con su velocidad de acuerdo con la
expresión
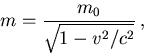
donde
donde ![]() es la fuerza aplicada al electrón debido al campo
eléctrico.
es la fuerza aplicada al electrón debido al campo
eléctrico.