Problemas de Métodos Matemáticos I

Curso 2003-2004.   Hoja 3



  1. Ecuaciones exactas. Se dice que la ecuación $R(x)\,y'' + P(x)\,y' + Q(x)\,y = 0$ es exacta si es posible escribirla en la forma $[R(x)\,y']' + [f(x)\,y]' = 0\,,$ donde $f(x)$ debe determinarse en función de $R(x), \, P(x)$ y $Q(x)$. Esta última ecuación puede integrarse inmediatamente, con lo que se obtiene una ecuación lineal de primer orden para $y$, que es posible resolver con lo métodos usuales. Al igualar los coeficientes de las ecuaciones precedentes y eliminar $f(x)$, demostrar que una condición necesaria para la exactitud es $R''(x) - P'(x) + Q(x) = 0$. Es posible demostrar que ésta es también una condición suficiente.

    En cada uno de los casos siguientes, aplicar el resultado anterior para determinar si la ecuación dada es exacta. En caso afirmativo, resolverla.

    i) $y'' + x\,y' + y = 0$, ii) $y'' + 3x^2\,y' + x\,y = 0$,
    iii) $x\,y'' - (\cos x)\,y' + (\sin x)\,y = 0$, $x>0$, iv) $x^2\,y'' + x\,y' - y = 0$, $x>0$ .

  2. Cambio de variables. A menudo una ecuación diferencial con coeficientes variables, $y'' + p(x)\,y' + q(x)\,y = 0$, puede escribirse en una forma más apropiada para hallar una solución al hacer un cambio de las variables independiente o dependiente, o ambas cosas.

    Determinar las condiciones sobre $p$ y $q$ tales que, por un cambio de la variable independiente, la ecuación se puede escribir como una ecuación con coeficientes constantes. Sea $z=u(x)$ la nueva variable independiente.

    a) Demostrar que

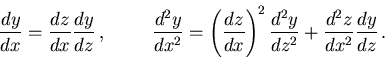
    \begin{displaymath}{dy\over dx} = {dz\over dx}{dy\over dz}\,, \hspace{1cm} {d^2y... ...}\right)^2 {d^2y\over dz^2} + {d^2z\over dx^2} {dy\over dz}\,.\end{displaymath}

    b) Demostrar que la ecuación diferencial queda escrita

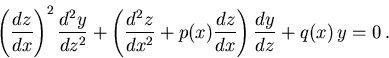
    \begin{displaymath}\left({dz\over dx}\right)^2 {d^2y\over dz^2} + \left({d^2z\over dx^2} + p(x){dz\over dx}\right){dy\over dz} + q(x)\,y = 0\,.\end{displaymath}

    c) Para que la ecuación resultante tenga coeficientes constantes, los coeficientes de $d^2y/dz^2$ y de $y$ deben ser proporcionales. Si $q(x)>0$, entonces es posible elegir la constante de proporcionalidad igual a uno, con lo que resulta

    \begin{displaymath}z = u(x) = \int \!dx\,[q(x)]^{1/2}\,.\end{displaymath}

    d) Con esta nueva variable $z$ demostrar que el coeficiente de $dy/dz$ también es una constante, siempre que la expresión

    \begin{displaymath}{q'(x) + 2p(x)\,q(x)\over2[q(x)]^{3/2}}\end{displaymath}

    sea constante. ¿Cómo debe modificarse este resultado para $q(x)<0$?

  3. En cada uno de los problemas siguientes, aplicar el método del problema anterior para transformar la ecuación dada en una con coeficientes constantes. En caso de ser posible, hallar la solución general de la ecuación dada.

    i) $y'' + x\,y' + e^{-x^2} y = 0$, $-\infty < x < \infty$,
    ii) $y'' + 3x\,y' + x^2\,y = 0$, $-\infty < x < \infty$,
    iii) $x\,y'' + (x^2-1)\,y' + x^3\,y = 0$, $0 < x < \infty$ .

  4. Ecuaciones de Euler. Una ecuación de la forma

    \begin{displaymath}x^2\,y'' + \alpha x\,y' + \beta\,y = 0\,, \hspace{1cm} x>0\,,\end{displaymath}

    con $\alpha$ y $\beta$ constantes reales, se conoce como ecuación de Euler. Demostrar que la sustitución $z=\ln x$ transforma la ecuación de Euler en una ecuación con coeficientes constantes.

    En cada uno de los casos siguientes, aplicar el método anterior para resolver la ecuación dada, para $x>0$.

    i) $x^2\,y'' + x\,y' + y = 0$, ii) $x^2\,y'' + 4x\,y' + 2 y = 0$,
    iii) $x^2\,y'' + 3x\,y' + 1.25 y = 0$, iv) $x^2\,y'' - 4x\,y' - 6y = 0$,
    v) $x^2\,y'' - 3x\,y' + 4 y = 0$, vi) $x^2\,y'' + 2x\,y' + 0.25y = 0$.

  5. Si las funciones $y_1$, $y_2$ son soluciones linealmente independientes de $y'' + p(x)\,y' + q(x)\,y = 0$, demostrar que entre ceros consecutivos de $y_1$ existe uno y sólo un cero de $y_2$. Observar que este resultado queda ilustrado por las soluciones $y_1(x) = \cos x$ e $y_2(x) = \sin x$ de la ecuación $y'' + y = 0$.

  6. Comportamiento asimptótico de las soluciones.

    a) Si $a, \ b$ y $c$ son constantes positivas, demostrar que todas las soluciones de la ecuación $a\,y'' + b\,y' + c\,y = 0$ tienden a cero cuando $x\to\infty$.

    b) Si $a>0$ y $c>0$, pero $b=0$, demostrar que el resultado del apartado anterior deja de ser cierto, pero que todas las soluciones son acotadas cuando $x\to\infty$.

    c) Si $a>0$ y $b>0$, pero $c=0$, demostrar que el resultado del apartado a) deja de ser cierto, pero que todas las soluciones tienden a una constante que depende de las condiciones iniciales cuando $x\to\infty$. Determinar esa constante para las condiciones iniciales $y(0) = y_0$, $y'(0) = y'_0$.

    d) Demostrar que $y=\sin x$ es una solución de

    \begin{displaymath}y'' + (k\,\sin^2x)\,y' + (1-k\,\cos x\,\sin x)\,y = 0\end{displaymath}

    para cualquier valor de la constante $k$. Si $0<k<2$, demostrar que $1-k\,\cos x\,\sin x > 0$ y que $k\,\sin^2x \geq 0$. Por tanto, observar que aún cuando los coeficientes de esta ecuación diferencial con coeficientes variables son no negativos (y el coeficiente de $y'$ se anula sólo en los puntos $x=0,\,\pi,\,2\pi,\dots$), tiene una solución que no tiende a cero cuando $x\to\infty$.

  7. En cada uno de los problemas siguientes, encontrar la solución del problema con valor inicial dado,

    i) $y'' + y' - 2y = 2x$, $y(0) = 0\,, \ y'(0) = 1$,
    ii) $y'' + 4 y = x^2 + 3e^x$, $y(0) = 0\,, \ y'(0) = 2$,
    iii) $y'' - 2y' + y = 4 + x\,e^x$, $y(0) = 1\,, \ y'(0) = 1$,
    iv) $y'' - 2y' - 3y = 3x\,e^{2x}$, $y(0) = 1\,, \ y'(0) = 0$,
    v) $y'' + 4 y = 3\sin 2x$, $y(0) = 2\,, \ y'(0) = -1$,
    vi) $y'' + 2y' + 5y = 4 e^{-x}\cos 2x$, $y(0) = 1\,, \ y'(0) = 0$.

  8. Determinar la solución general de

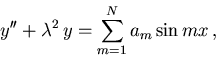
    \begin{displaymath}y'' + \lambda^2\,y = \sum_{m=1}^N a_m \sin mx\,,\end{displaymath}

    donde $\lambda > 0$ y $\lambda \neq m$ para $m=1,\dots,N$.

  9. En este problema se indica un método alternativo para resolver la ecuación

    \begin{displaymath}y'' + b\,y' + c\,y = (D^2 + b\,D + c)\,y = g(x)\,,\end{displaymath}

    donde $b$ y $c$ son constantes, y $D$ denota derivación respecto a $x$. Sean $r_1$ y $r_2$ los ceros del polinomio característico de la ecuación homogénea correspondiente. Estas raíces pueden ser números reales y diferentes, reales e iguales o complejos conjugados.

    a) Comprobar que la ecuación puede escribirse de la forma factorizada

    \begin{displaymath}(D-r_1)(D-r_2)\,y = g(x)\,,\end{displaymath}

    donde $r_1+r_2 = -b$, y $r_1r_2 = c$.

    b) Sea $u=(D-r_2)\,y$. Demostrar que la solución de la ecuación de segundo orden puede calcularse resolviendo las dos ecuaciones de primer orden siguientes:

    \begin{displaymath}(D-r_1)\,u= g(x)\,, \hspace{1cm} (D-r_2)\,y = u(x)\,.\end{displaymath}

    En cada uno de los casos siguientes, aplicar el método anterior para resolver la ecuación diferencial dada

    i) $y'' - 3y' - 4y = e^{2x}$, ii) $2y'' + 3y' + y = x^2 + 3\sin x$,
    iii) $y'' + 2y' + y = 2 e^{-x}$, iv) $y'' + 2y' = 3 + 4\sin 2x$.

  10. En muchos problemas físicos el término no homogéneo puede especificarse mediante diferentes fórmulas en distintos periodos. Por ejemplo, determinar la solución de

    \begin{displaymath}y'' + y = \left\{\begin{array}{lr}t\,, & 0\leq t \leq \pi\,, \\ [1mm] \pi\,e^{\pi-t}\,, & t>\pi\,,\end{array}\right.\end{displaymath}

    que satisfaga las condiciones iniciales $y(0) = 0\,, \ y'(0) = 1$. Suponer que $y$ e $y'$ también son continuas en $t=\pi$. Trazar la gráfica del término no homogéneo y de la solución como funciones del tiempo $t$.

    [Ayuda: Primero resolver el problema con valor inicial para $t\leq\pi$; luego para $t>\pi$, determinando las constantes de esta última solución a partir de las condiciones de continuidad en $t=\pi$.]

  11. a) Demostrar que

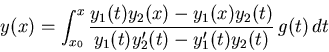
    \begin{displaymath}y(x) = \int_{x_0}^x {y_1(t)y_2(x) - y_1(x)y_2(t)\over y_1(t)y'_2(t) - y'_1(t)y_2(t)}\,g(t)\,dt\end{displaymath}

    es una solución del problema con valor inicial

    \begin{displaymath}\hspace{2.5cm} L[y]=g(x)\,, \hspace{1.5cm} y(x_0) = 0\,, \ y'(x_0) = 0\,, \hspace{5cm} (1)\end{displaymath}

    donde $y_1,\ y_2$ son dos soluciones linealmente independientes de la ecuación homogénea $L[y]=0$.

    b) Demostrar que la solución del problema con valor inicial (1) con $L[y] = y'' + y$ es

    \begin{displaymath}y = \int_{x_0}^x \sin(x-t)\,g(t)\,dt\,.\end{displaymath}

    c) Encontrar la solución del problema con valor inicial

    \begin{displaymath}y'' + y= g(x)\,, \hspace{1cm} y(0) = y_0\,, \ y'(0) = y'_0\,.\end{displaymath}

    d) Encontrar la solución del problema con valor inicial (1) con $L[y] = (D-a)(D-b)\,y$, donde $a\neq b$ son números reales.

    e) Encontrar la solución del problema con valor inicial (1) con
    $L[y] = [D^2 - 2\lambda D + (\lambda^2 + \mu^2)]\,y$. Observar que las raíces de la ecuación característica son $\lambda\pm i\mu$.

    f) Encontrar la solución del problema con valor inicial (1) con $L[y] = (D-a)^2y$, donde $a$ es un número real cualquiera.

    g) Combinando los apartados anteriores, demostrar que la solución del problema con valor inicial (1) con $L[y] = (a\,D^2 + b\,D + c)\,y$, donde $a$, $b$ y $c$ son constantes, tiene la forma

    \begin{displaymath}y = \int_{x_0}^x K(x-t)\,g(t)\,dt\,.\end{displaymath}

    La función $K$ depende sólo de las soluciones $y_1,\ y_2$ de la ecuación homogénea y es independiente del término no homogéneo. Una vez determinado $K$, todos los problemas no homogéneos del mismo operador diferencial $L$ se reducen a la evaluación de la integral, que recibe el nombre de convolución de $K$ y $g$, y la función $K$ se denomina el kernel (núcleo, en alemán) de la ecuación.


Juan García-Bellido

Thu Sep 25 12:27:33 BST 2003