Problemas de Métodos Matemáticos I

Curso 2003-2004.   Hoja 5



  1. Fórmula de Abel. Demostrar por inducción que el Wronskiano de las soluciones de la ecuación lineal $\ {\bf x}' = {\bf A}(t){\bf x}\ $, está dado por

    \begin{displaymath}W({\bf x}_1, \dots, {\bf x}_n) = c\,\exp\,\int\!{\rm tr}{\bf A}(t)\,dt\,,\end{displaymath}

    donde ${\bf A}(t)$ es una matriz $n\times n$, y $c$ es una constante.



  2. Sea la ecuación de segundo órden $y'' + p(t)\,y' + q(t)\,y = 0$.

    a) Demostrar que es equivalente al sistema de ecuaciones

    \begin{displaymath}{\bf x}' = {\bf A}(t){\bf x}\,, \hspace{1cm} {\rm con} \hspac... ...egin{array}{cc}0 & 1\\ [4mm] -q(t) & -p(t)\end{array}\right)\,.\end{displaymath}

    b) Demostrar que si $\{{\bf x}_1,\,{\bf x}_2\}$ forman un conjunto fundamental de soluciones del sistema de ecuaciones y si $\{y_1,\,y_2\}$ son un conjunto fundamental de soluciones de la ecuación de segundo órden, entonces

    \begin{displaymath}W(y_1,\,y_2) = c\,W({\bf x}_1,\,{\bf x}_2)\,,\end{displaymath}

    donde $c$ es una constante.

    c) Suponer que ${\bf A}(t)$ es una matriz $2\times2$ con coeficientes constantes, asociada a una ecuación de segundo órden. Determinar la ecuación característica en ambos casos y compararlas.



  3. Ecuación de Euler.

    a) Demostrar que la ecuación de Euler de segundo órden

    \begin{displaymath}a\,t^2\,y'' + b\,t\,y' + c\,y = 0\,,\end{displaymath}

    con $a$, $b$ y $c$ constantes reales, es equivalente a un sistema de ecuaciones de la forma $t\,{\bf x}' = {\bf A}{\bf x}$. Determinar la matriz $\,{\bf A}$.

    b) Suponer el Ansatz $\,{\bf x}(t) = {\bf v}\,t^{\,r}\,$ para la forma general de la solución de dicho sistema, donde ${\bf v}$ es un vector constante, y demostrar que satisface la ecuación de autovectores

    \begin{displaymath}({\bf A} - r {\bf 1\!l})\,{\bf v}=0\,.\end{displaymath}

    c) Para que existan soluciones no triviales del sistema, demostrar que $r$ debe satisfacer la ecuación

    \begin{displaymath}{\rm det}({\bf A} - r {\bf 1\!l}) = 0\,.\end{displaymath}

    Comparar con la ecuación característica de la ecuación de Euler, y encontrar la solución general del sistema de ecuaciones.

  4. Calcular la ecuación característica de la matriz de coeficientes ${\bf A}$ del sistema

    \begin{displaymath}{\bf x}' = \left(\begin{array}{rrrr}2 & 0 & -8 & -3\\ [2mm]-1... ...-25 & -9\\ [2mm]33 & 10 & 90 & 32\end{array}\right)\,{\bf x}\,.\end{displaymath}

    Confirmar que ${\bf A}$ tiene repetido un par complejo conjugado de autovalores $\lambda_1 = \lambda_2^*$. Encontrar la cadena de autovectores generalizados asociada al autovalor $\lambda_1$. A continuación calcular cuatro soluciones linealmente independientes de valores reales del sistema ${\bf x}' = {\bf A\,x}$.

  5. Circuitos eléctricos.

    a) Demostrar usando las leyes de Kirchhoff que el circuito eléctrico de la figura














    satisface el sistema de ecuaciones diferenciales

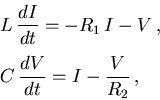
    \begin{displaymath}\begin{array}{l}{\displaystyle L\,{dI\over dt} = -R_1\,I - V}... ...\displaystyle C\,{dV\over dt} = I - {V\over R_2}\,,}\end{array}\end{displaymath}

    donde $I$ es la corriente que pasa por la bobina y $V$ es la caida de potencial a través del condensador.

    b) Hallar una condición sobre $R_1$, $R_2$, $L$ y $C$ tal que los autovalores de la matriz del sistema sean reales y diferentes.

    c) Demostrar que en ese caso los dos autovalores son negativos. Entonces demostrar que $I(t) \to 0$ y $V(t) \to 0$ cuando $t \to \infty$, independientemente de las condiciones iniciales.

    d) Si no se satisface dicha condición, entonces los autovalores son complejos o bien son iguales. ¿Qué se puede decir entonces sobre el límite de $I(t)$ y $V(t)$ cuando $t \to \infty$?

    e) Sea el circuito de la figura, con $R_1=1\Omega$, $R_2=5\Omega$, $L=1$ H y $C=0.2$ F. Encontrar la corriente y el potencial para todo tiempo, sabiendo que en el instante inicial $I(0)=1$ A y $V(0)=2$ V.

    f) Con los datos del apartado e), ¿Cuánto tardará la corriente en caer a cero por primera vez? ¿Qué vale el potencial en ese instante? ¿Cuánto tardará el potencial en caer a cero por primera vez? ¿Qué vale la corriente en ese instante? Dibujar en el plano $(I,\,V)$ la evolución temporal del sistema.

  6. Una partícula de masa $m$ y carga eléctrica $q$ se mueve con velocidad ${\bf v}$ en el plano $(x,\,y)$, bajo la influencia de un campo magnético uniforme paralelo al eje $z$, ${\bf B} = B\, {\bf e_z}$, de modo que la fuerza de Lorentz que actúa sobre la partícula esta dada por ${\bf F} = q\,{\bf v}\times {\bf B}$.

    a) Demostrar que las ecuaciones del movimiento de la partícula son

    \begin{displaymath}\begin{array}{l}m\,x'' = q\,B\,y'\,,\\ [3mm]m\,y'' = -q\,B\,x'\,.\end{array}\end{displaymath}

    b) Demostrar que la partícula sigue un movimiento circular con frecuencia angular (de Larmor) $\omega = qB/m$. Demostrar que la energía de la partícula se conserva, a pesar de que la fuerza es proporcional a la velocidad.

    c) Suponiendo que la partícula parte del punto ${\bf x} = (r_0,\,0)$, con velocidad ${\bf x}' = (0,\,\omega\,r_0)$, demostrar que la trayectoria de la partícula es una circunferencia de radio $r_0$.

    d) Si además del campo magnético, la partícula cargada se mueve bajo la influencia de un campo eléctrico uniforme en la dirección del eje $x$, ${\bf E} = E\,{\bf e_x}$, entonces la fuerza de Lorentz que actua sobre ella es ${\bf F} = q\,({\bf E} + {\bf v}\times{\bf B})$.
    Suponer que la partícula parte en reposo del origen. Demostrar que la trayectoria de la partícula es la cicloide escrita en forma paramétrica

    \begin{displaymath}\begin{array}{l}x = a(1-\cos\omega t)\,,\\ [3mm]y = a(\omega t - \sin\omega t) \,,\end{array}\end{displaymath}

    donde $a = E/\omega B$ y $\omega = qB/m$.

  7. Dos vagones de tren están unidos como en la figura














    conectados por un muelle fijo de constante $k$ y un amortiguador que ejerce fuerzas opuestas sobre los vagones, de magnitud proporcional a su velocidad relativa, $\gamma\,(x_1' - x_2')$. Los dos vagones están además sometidos a fuerzas de rozamiento (del aire) proporcionales a sus velocidades respectivas, $\gamma_1\,x_1'$ y $\gamma_2\,x_2'$. Aplicar la segunda ley de Newton para obtener las ecuaciones de movimiento

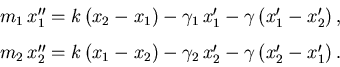
    \begin{displaymath}\begin{array}{l}m_1\,x_1'' = k\,(x_2-x_1) - \gamma_1\,x_1' - ... ..._1-x_2) - \gamma_2\,x_2' - \gamma\, (x_2' - x_1')\,.\end{array}\end{displaymath}

    Estas ecuaciones pueden escribirse en forma matricial

    \begin{displaymath}{\bf M}\,{\bf x}'' = {\bf K}\,{\bf x} + {\bf R}\,{\bf x}'\,,\end{displaymath}

    donde las matrices de masa, de rigidez y de rozamiento están dadas por

    \begin{displaymath}{\bf M} = \left(\begin{array}{cc}m_1 & 0\\ [3mm]0 & m_2\end{a... ...\gamma\\ [3mm] \gamma & -(\gamma+\gamma_2)\end{array}\right)\,.\end{displaymath}

    a) Mediante el cambio de variables $\{x_1(t),\,x_2(t),\,x_3(t)=x_1'(t),\, x_4(t)=x_2'(t)\}$, convertirlo en un sistema de cuatro ecuaciones de primer órden, de la forma ${\bf x}' = {\bf A}\,{\bf x}$, con $A$ una matriz $4\times4$.

    b) Tomando $m_1 = m_2 = 1$ kg, $\gamma_1 = \gamma_2 = 2\gamma = 2$ N.s/m y $k = 2$ N/m, calcular las cuatro soluciones linealmente independientes del sistema de ecuaciones. Interpretar físicamente los distintos modos. Calcular la solución para todo tiempo, suponiendo que las masas empiezan en la posición de equilibrio con velocidad $v_0=10$ m/s. ¿Qué distancia han recorrido en 5 s? ¿Cuánto espacio recorrerán antes de detenerse? Comentar.

    c) Encontrar las posiciones de los vagones a todo tiempo si $m_1 = m_2 = 1$ kg, $\gamma_1 = \gamma_2 = \gamma = 1$ N.s/m y $k = 1$ N/m, y las condiciones iniciales son $x_1(0)=x_2(0)=0$, $x_1'(0)=x_2'(0)=v_0$. ¿Qué distancia recorrerán antes de deternerse? Repetir el cálculo suponiendo que el vagón 1 está protegido contra la resistencia del aire por el segundo vagón, de modo que ahora $\gamma_1=0$. Demostrar que antes de deternerse los vagones viajan el doble de rápido que en el caso anterior.

  8. Dos cuerpos de masa $m$ están sujetos a un resorte bajo tensión constante $T$ como en la figura














    Suponer que las masas oscilan verticalmente con amplitudes tan pequeñas que los senos de los ángulos pueden ser aproximados por sus tangentes.

    a) Demostrar que los desplazamientos $y_1\,,\ y_2$ de las dos masas satisfacen

    \begin{displaymath}\begin{array}{l}c\,y_1'' = -2\,y_1 + y_2\,,\\ [3mm]c\,y_2'' = y_1 - 2\,y_2\,,\end{array}\end{displaymath}

    donde $c=mL/T$.

    b) Encontrar los modos normales de vibración y las frecuencias correspondientes.

    c) Si las masas parten de su posición de equilibrio con velocidades iguales y opuestas, $y_1'(0) = v_0\,,\ y_2'(0) = - v_0$, determinar la posición del sistema a todo tiempo.

    d) De cada cuerpo se cuelga otra masa $m$, sujeta a través de un muelle de constante de recuperación $k$, que induce una fuerza externa vertical y hacia abajo $F_{\rm ext} = mg\,\cos\omega t$, con $\omega=\sqrt{k/m}$. Calcular la solución a todo tiempo suponiendo $m=1$ kg, $T=1$ N, $L=1$ m, $k=4$ N/m. ¿Qué ocurriría en caso de que $k=3$ N/m?

  9. Suponer que la trayectoria $(x(t)\,,\ y(t))$ de una partícula que se mueve en el plano satisface el problema de condiciones iniciales

    \begin{displaymath}\begin{array}{l}x'' - 2\,y' + 3x = 0\,,\\ [3mm]y'' + 2\,x' + ... ...\,,\\ [3mm] x(0) = 4\,,\ y(0) = x'(0) = y'(0) = 0\,.\end{array}\end{displaymath}

    Resolver el problema y verificar que la solución describe el hipocicloide que traza un punto $P(x,y)$ fijo en la circunferencia de un círculo de radio unidad que rueda alrededor del interior de un círculo de radio $a=4$. Si $P$ empieza en el punto $(a\,,\ 0)$ cuanto $t=0$, entonces el parámetro $t$ representa el ángulo que aparece en la figura.














  10. Vibraciones inducidas por terremotos en edificios de muchos pisos. Vamos a estudiar la respuesta a un terremoto (oscilación horizontal del suelo) de un edificio de siete plantas, cada una de las cuales tiene una masa de una tonelada. Considerar una fuerza horizontal restauradora de $k = 10$ kN/m entre pisos adyacentes. Es decir, las fuerzas internas que aparecen como respuesta a los desplazamientos horizontales del piso $i$-esimo son $F_i = k\, (x_{i+1} - x_i) - k\,(x_i - x_{i-1})$.

    a) Deducir que las oscilaciones transversales libres del conjunto de pisos satisfacen la ecuación ${\bf x}'' = {\bf A}\,{\bf x}$, con ${\bf A}$ una matriz $7\times7$ constante.

    b) Calcular los autovalores de ${\bf A}$, las frecuencias naturales y los periodos de oscilación de cada modo normal. Comprobar que un terremoto típico que produce oscilaciones del suelo con periodo de 2 s es incómodamente próximo a la quinta frecuencia natural de 1.9869 s del edificio de 7 plantas.

    c) Una oscilación del suelo $E\,\cos\omega t$, con amplitud $E$ y aceleración $a = -E\omega^2\,\cos\omega t$, produce una fuerza de inercia opuesta, $F=-ma = mE\omega^2\,\cos\omega t$, en cada piso. El sistema no homogéneo resultante es

    \begin{displaymath}{\bf x}'' = {\bf A}\,{\bf x} + (E\omega^2\,\cos\omega t)\,{\bf b}\,,\end{displaymath}

    donde ${\bf b}=(1\,,\ 1\,,\ 1\,,\ 1\,,\ 1\,,\ 1\,,\ 1)$. Pintar la amplitud de oscilación máxima de las ocilaciones forzadas de un piso cualquiera como función del período de las vibraciones del terremoto. Comprobad que mientras es posible que un temblor de tierra con periodo 2 s pudiera inducir vibraciones de resonancia destructivas en el edificio, éste probablemente no correría ningún riesgo con un temblor de periodo 2.5 s. Edificios diferentes tienen frecuencias naturales de ocilación diferentes, de modo que un terremoto dado puede demoler un edificio, sin afectar al vecino. Esta anomalía ha sido observada muchas veces.

  11. El automóvil de dos ejes. Consideremos un modelo realista de automóvil con dos ejes y un sistema de suspensión delantero y trasero separados, como se observa en la figura.














    Supongamos que el cuerpo del automóvil actúa como lo haría una barra sólida de masa $m$ y longitud $L = L_1 + L_2$. Dicho cuerpo tiene un momento de inercia $I$ respecto a su centro de gravedad $C$ que se encuentra a una distancia $L_1$ del extremo frontal del vehículo. El automóvil tiene muelles de suspensión delanteros y traseros cuyas constantes de Hooke son $k_1$ y $k_2$ respectivamente. Cuando el vehículo está en movimiento, sea $x(t)$ el desplazamiento vertical del centro de masa respecto a su posición de equilibrio; y sea $\theta(t)$ su desplazamiento angular (en radianes) fuera de la horizontal.

    a) Usando las leyes de Newton para la aceleración lineal y angular, deducir las ecuaciones

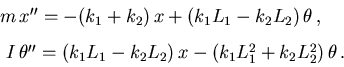
    \begin{displaymath}\begin{array}{l}m\,x'' = - (k_1 + k_2)\,x + (k_1 L_1 - k_2 L_... ... - k_2 L_2)\,x - (k_1 L_1^2 + k_2 L_2^2)\,\theta \,.\end{array}\end{displaymath}

    b) Suponer $m=1000$ kg, $L_1=1$ m, $L_2=3$ m, $I=2000$ kg.m$^2$ y $k_1 = k_2 = 40$ kN/m. Calcular las dos frecuencias naturales de oscilación, $\omega_1$ y $\omega_2$, del automóvil.

    c) Suponer que se conduce el coche a una velocidad de $v$ m/s a lo largo de una carretera con baches de longitud de onda de 100 m. El resultado es una fuerza periódica externa sobre el sistema de suspensión del coche con frecuencia $\omega=2\pi\,v/100$ rad/s. Calcular las dos velocidades críticas del coche para las cuales entra en resonancia.

    d) Suponer que $k_1=k_2=k$ y $L_1=L_2=L/2$ (la situación simétrica). Demostrar que toda oscilación libre es una combinación de una oscilación vertical con frecuencia $\omega_1 = \sqrt{2k/m}$ y una oscilación angular de frecuencia $\omega_2 = \sqrt{kL^2/2I}$.

  12. Sea el circuito eléctrico de la figura














    a) Usar las leyes de Kirchhoff para deducir el sistema de ecuaciones

    \begin{displaymath}{d\over dt}\left(\begin{array}{c}I\\ [3mm]V\end{array}\right)... ...y}\right) \left(\begin{array}{c}I\\ [3mm]V\end{array}\right)\,,\end{displaymath}

    donde $I$ es la corriente que pasa por la bobina y $V$ es la caída de potencial a través del condensador.

    b) Demostrar que los autovalores de la matriz de coeficientes son reales y diferentes si $L > 4CR^2$; y complejos conjugados si $L < 4CR^2$.

    c) Suponer que $R=1\Omega$, $C=0.5$ F y $L=1$ H. Encontrar la solución general del sistema en este caso.

    d) Encontrar $I(t)$ y $V(t)$ si $I(0)=2$ A y $V(0)=1$ V.

    e) Determinar los valores límite de $I(t)$ y $V(t)$ cuando $t \to \infty$. ¿Dependen estos valores de las condiciones iniciales?

    f) Suponer que se acopla una fuente de alimentación que suministra una corriente externa $I_{\rm ext}(t) = 2\,\exp(-t)$ A. Determinar la solución del sistema que satisface las condiciones iniciales $I(0)=V(0)=0$.


Juan García-Bellido

Thu Sep 25 12:32:04 BST 2003