prob6

Problemas de Métodos Matemáticos I

Curso 2003-2004. Hoja 6

Calcular los puntos críticos del sistema

$\begin{displaymath}\begin{array}{l}{\displaystyle {dx\over dt} = 3\,x-x^2-x\,y}\... ...m] {\displaystyle {dy\over dt} = y + y^2 - 3x\,y}\,.\end{array}\end{displaymath}$

Estudiar su estabilidad y dibujar un retrato del espacio de fases.
Considerar el sistema casi lineal

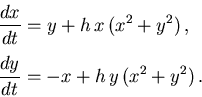
$\begin{displaymath}\begin{array}{l}{\displaystyle {dx\over dt} = y + h\,x\,(x^2+... ...displaystyle {dy\over dt} = -x + h\,y\,(x^2+y^2)}\,.\end{array}\end{displaymath}$

a) Demostrar que el origen es un punto centro del sistema lineal correspondiente ().
b) Suponer que $h\neq0$ . Reescribir el sistema de ecuaciones diferenciales en coordenadas polares.
c) Suponer que . Integrar la ecuación diferencial radial y estudiar el comportamiento de cuando $t\to+\infty$ . ¿Qué se puede decir del carácter del punto crítico $(0,\,0)$ ?
d) Suponer que . Hacer lo mismo que en el apartado anterior.
En el caso de un sistema de dos dimensiones que no es lineal, las trayectorias cerca de un punto crítico aislado pueden presentar una estructura considerablemente más complicada que cerca de nodos, centros, puntos silla y espiral. Por ejemplo, considerar el sistema

$\begin{displaymath}\begin{array}{l}{\displaystyle {dx\over dt} = x\,(x^3-2y^3)}\... ...4mm] {\displaystyle {dy\over dt} = y\,(2x^3-y^3)}\,.\end{array}\end{displaymath}$

Este sistema no es casi lineal ya que el origen no es un punto crítico aislado del sistema lineal trivial asociado ( $x'=0,\ y'=0$ ). Resolver la ecuación homogénea de primer orden

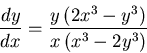
$\begin{displaymath}{dy\over dx} = {y\,(2x^3-y^3)\over x\,(x^3-2y^3)}\end{displaymath}$

y demostrar que las trayectorias del sistema son Hojas de Descartes de la forma

$\begin{displaymath}x^3 + y^3 = 3c\,x\,y\,,\end{displaymath}$

donde es una constante arbitraria. Dibujar un retrato del espacio de fases.
Especies en competencia. Supervivencia de una sola especie. Considerar dos especies cuyas poblaciones son $x(t),\ y(t)$ , en el instante , y que compiten por los mismos alimentos en un nicho ecológico común. La dinámica de estas dos poblaciones viene caracterizada por el sistema de ecuaciones

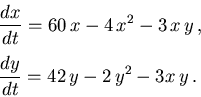
$\begin{displaymath}\begin{array}{l}{\displaystyle {dx\over dt} = 60\,x-4\,x^2-3\... ...splaystyle {dy\over dt} = 42\,y - 2\,y^2 - 3x\,y}\,.\end{array}\end{displaymath}$

Calcular los puntos críticos, estudiar su estabilidad y dibujar un retrato del espacio de fases. Mostrar que existe una linea separatriz en el espacio de fases que separa dos regiones en las que sólo una de las dos especies sobrevive finalmente.
Especies en competencia. Coexistencia pacífica. Dos especies cuyas poblaciones son $x(t),\ y(t)$ , en el instante , compiten por los mismos alimentos en un nicho ecológico común. La dinámica de estas dos poblaciones viene caracterizada por el sistema de ecuaciones

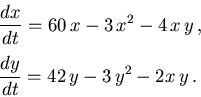
$\begin{displaymath}\begin{array}{l}{\displaystyle {dx\over dt} = 60\,x-3\,x^2-4\... ...splaystyle {dy\over dt} = 42\,y - 3\,y^2 - 2x\,y}\,.\end{array}\end{displaymath}$

Calcular los puntos críticos, estudiar su estabilidad y dibujar un retrato del espacio de fases. Demostrar que, a diferencia del problema anterior, es posible la coexistencia pacífica de las dos especies.
Sistemas depredador-presa. Equilibrio estable. Una especie de depredadores se alimenta de otra, la presa , que a su vez se nutre de un tercer alimento ampliamente disponible en el sistema. La dinámica de estas dos poblaciones viene caracterizada por el sistema de ecuaciones

$\begin{displaymath}\begin{array}{l}{\displaystyle {dx\over dt} = 5\,x-x^2-\,x\,y... ...[4mm] {\displaystyle {dy\over dt} = -2\,y + x\,y}\,.\end{array}\end{displaymath}$

Calcular los puntos críticos, estudiar su estabilidad y dibujar un retrato del espacio de fases. Demostrar que es posible que las presas y los depredadores coexistan con poblaciones en equilibrio estable.
Sistemas depredador-presa. Equilibrio inestable. Una especie de depredadores se alimenta de otra, la presa , que a su vez se nutre de un tercer alimento ampliamente disponible en el sistema. La dinámica de estas dos poblaciones viene caracterizada por el sistema de ecuaciones

$\begin{displaymath}\begin{array}{l}{\displaystyle {dx\over dt} = x^2 - 2\,x - \,... ...] {\displaystyle {dy\over dt} = y^2 -4\,y + x\,y}\,.\end{array}\end{displaymath}$

Calcular los puntos críticos, estudiar su estabilidad y dibujar un retrato del espacio de fases. Demostrar que para cada una de estas especies no hay más alternativa que crecer sin cota alguna o la extinción.
Vibraciones no lineales amortiguadas. En ocasiones es posible estimar las correcciones no lineales a la ley de Hooke para la fuerza que ejerce un muelle sobre un objeto de masa , $F = - k\,x - \beta\,x^3$ , sometido a una fuerza de rozamiento $F_{\rm R} = - \gamma\,x'$ . Considerar el caso kg, N/m, $\beta = 5/4$ N/m, $\gamma = 2$ N.s/m.
a) Escribir las ecuaciones del movimiento en forma de un sistema de dos ecuaciones de primer órden.
b) Estudiar los puntos críticos del sistema en ausencia de rozamiento, $\gamma=0$ , así como su estabilidad. Dibujar un retrato del espacio de fases y determinar las separatrices.
c) Hacer lo mismo que en el apartado anterior pero en presencia de rozamiento. ¿Cómo se modifican las separatrices?
Una partícula de masa unidad se mueve en un potencial

$\begin{displaymath}V(x) = 2\,x^2 - {1\over 3}x^3\,.\end{displaymath}$

Determinar los puntos críticos de la dinámica de la partícula, el retrato del espacio de fases, y buscar la correspondencia de las trayectorias con la forma del potencial.
Una partícula de masa unidad se mueve en un pozo doble de potencial

$\begin{displaymath}V(x) = {1\over4}\,(x^2 - 1)^2\,.\end{displaymath}$

Determinar los puntos críticos de la dinámica de la partícula, el retrato del espacio de fases, y buscar la correspondencia de las trayectorias con la forma del potencial. ¿Cuál es el período de una partícula que empieza en reposo en $x=\sqrt2$ ?

Juan García-Bellido

Thu Sep 25 12:35:53 BST 2003