


Next: Átomos
multielectrónicos. El sistema Up: cuantica2 Previous: El átomo de
hidrógeno.
1. Demostrar que la
relación
donde 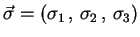 son
las matrices de Pauli, y
son
las matrices de Pauli, y 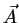 y
y 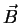 son operadores vectoriales que conmutan con
son operadores vectoriales que conmutan con 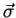 , pero
no necesariamente entre ellos.
, pero
no necesariamente entre ellos.
2. Sea 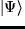 el estado de una partícula de spin
1/2. Se mide el valor medio de
el estado de una partícula de spin
1/2. Se mide el valor medio de 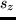 en ese estado y el
resultado es
en ese estado y el
resultado es 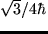 .
.
a) ¿Cuál es la probabilidad de que al medir 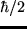 en el estado
en el estado 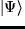 obtengamos como resultado
obtengamos como resultado 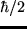 ? ¿Y
? ¿Y 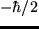 ?
?
b) Suponiendo que el valor medio de la proyección sobre el eje 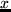 es
es 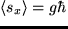 y que el coeficiente del estado
y que el coeficiente del estado 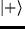 es real y positivo, ¿entre qué
límites puede variar
es real y positivo, ¿entre qué
límites puede variar 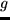 ?
?
c) Se mide 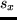 , y se obtienen como resultados de la medida
, y se obtienen como resultados de la medida 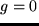 y
y 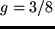 , pero el aparato no puede decidir entre ambos estados.
Escoger aquél de los dos valores que sea compatible con los
límites encontrados en el apartado anterior.
, pero el aparato no puede decidir entre ambos estados.
Escoger aquél de los dos valores que sea compatible con los
límites encontrados en el apartado anterior.
d) Calcular los valores posibles
que puede dar la medida del valor medio 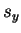 en el estado
en el estado 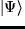 .
.
3. En una cierta base el operador asociado a la tercera
componente de spin para un sistema de spin 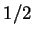 toma la forma:
toma la forma:
Comprobar que dicho operador puede, en efecto, representar el
observable 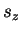 . Escoger, de entre las matrices
siguientes, una tal que con el
. Escoger, de entre las matrices
siguientes, una tal que con el 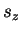 dado pueda
representar el observable
dado pueda
representar el observable 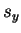 :
:
Encontrar, en la misma base en que están escritos 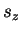 y
y 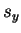 , la matriz asociada a
, la matriz asociada a 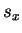 .
.
4. Un chorro de electrones que
se encuentran en el estado
se hace pasar por un aparato tipo Stern-Gerlach que mide la tercera
componente del spin.
a) ¿Qué porcentaje de electrones dará como
resultado de la medida 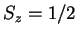 ? Si se gira el aparato de
modo que mida la componente
? Si se gira el aparato de
modo que mida la componente 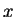 del spin, ¿qué
porcentaje de los electrones tendrá
del spin, ¿qué
porcentaje de los electrones tendrá 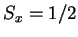 ?
?
b) Idem, pero con un chorro de electrones en el que el 50% se hallan en
el estado 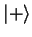 y el otro 50% en el
y el otro 50% en el 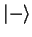 .
.
5. Una partícula de
spin 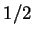 se encuentra en un estado
se encuentra en un estado 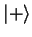 . ¿Cuál es la probabilidad de que
la proyección del spin sobre la dirección
. ¿Cuál es la probabilidad de que
la proyección del spin sobre la dirección 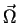 sea
sea 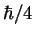 ? ¿Y
? ¿Y 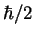 ?
?
6.Suponga
que la función de ondas de un electrón viene dada por:
con 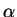 y
y 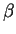 pertenecientes
a C. Determinar
pertenecientes
a C. Determinar 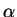 y
y 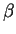 sabiendo que:
sabiendo que:
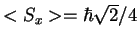 y
y 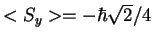
¿Cuál es la probabilidad de que al efectuar una medida
del valor de la proyección del espín del electrón
en la dirección (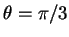 ,
, 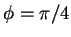 ) encontremos el valor
) encontremos el valor 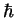 /2?
/2?
7. Demuestre que el estado
fundamental de dos electrones confinados en un potencial armónico
unidimensional tiene espín total cero.
8. Sea 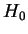 el hamiltoniano de una partícula. Supongamos que actúa
sólo sobre las variables espaciales y que tiene tres niveles
equidistantes de energías 0,
el hamiltoniano de una partícula. Supongamos que actúa
sólo sobre las variables espaciales y que tiene tres niveles
equidistantes de energías 0, 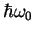 y
y 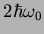 (
(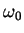 es una constante real y
positiva), que son no degenerados en el espacio orbital de estados, y
tienen degeneración
es una constante real y
positiva), que son no degenerados en el espacio orbital de estados, y
tienen degeneración 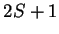 en el de spin (donde
en el de spin (donde 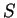 es el spin de la partícula). Consideraremos
sólo el espacio desarrollado por los tres autoestados de
es el spin de la partícula). Consideraremos
sólo el espacio desarrollado por los tres autoestados de 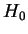 mencionados.
mencionados.
a) Considerar un sistema de tres electrones cuyo hamiltoniano es:
Encontrar los niveles de energía de 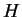 y el grado de
degeneración de cada uno de ellos.
y el grado de
degeneración de cada uno de ellos.
b) Lo mismo para un sistema de bosones idénticos de spin 0.
9. Considerar un sistema de 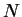 electrones encerrado en una caja tridimensional de lado
electrones encerrado en una caja tridimensional de lado 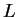 . Suponer que pueden despreciarse las interacciones entre
ellos y que no están sometidos a ningún potencial externo.
Construir el estado fundamental del sistema.
. Suponer que pueden despreciarse las interacciones entre
ellos y que no están sometidos a ningún potencial externo.
Construir el estado fundamental del sistema.
a) Calcular la máxima energía que puede tener un
electrón en dicho estado (energía de Fermi).
b) Deducir la densidad de estados 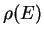 , definida
de modo que
, definida
de modo que 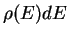 es el número de estados
individuales cuyas energías están entre
es el número de estados
individuales cuyas energías están entre 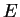 y
y 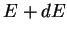 .
.
10. Dos partículas
idénticas de spin 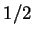 que no interactúan
entre sí están sometidas a un potencial tipo pozo cuadrado
unidimensional, infinito y de anchura
que no interactúan
entre sí están sometidas a un potencial tipo pozo cuadrado
unidimensional, infinito y de anchura 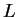 .
.
a) Calcular las funciones de onda de los estados correspondientes a los
tres valores más bajos de la energía.
b) Se introduce una perturbación
Calcular las correcciones a primer orden en teoría de
perturbaciones de las dos energías más bajas del
hamiltoniano sin perturbar.
11. La función de ondas
de dos partículas idénticas de espín 1/2 viene
dada por:
y es autoestado de un hamiltoniano que no contiene términos
dependientes del espín.
a) Escriba el hamiltoniano y la autoenergía del estado.
b) Describa y justifique la forma del autoestado y obtenga el valor
de su espín.
c) A partir de la autofunción dada, obtenga otra con
la misma energía y cuyo espín difiera del suyo en una
unidad de 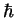 .
.
d) ¿Cuáles serían las autoenergías
más bajas del sistema si añadiéramos al
hamiltoniano un término 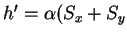 ) ?
) ?



Next: Átomos
multielectrónicos. El sistema Up: cuantica2 Previous: El átomo de
hidrógeno.
Enrique Perez Montero 2004-02-06
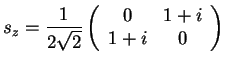
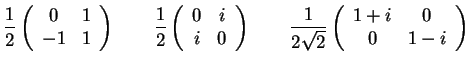
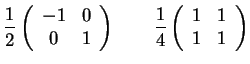
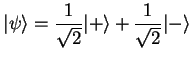
![]() y
y ![]() pertenecientes
a C. Determinar
pertenecientes
a C. Determinar ![]() y
y ![]() sabiendo que:
sabiendo que:![]() y
y ![]()
![]() ,
, ![]() ) encontremos el valor
) encontremos el valor ![]() /2?
/2? 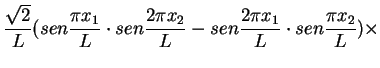
![]() .
. ![]() ) ?
) ?