Interacción de partículas con campos eléctricos y magnéticos.

1. Calcular, utilizando teoría de perturbaciones, la variación de la energía de los niveles $2s$ y $2p$ del átomo de hidrógeno al aplicarle un campo eléctrico constante en la dirección del eje $x$. (Efecto Stark).

2. Sea una partícula de spin $1/2$ y momento magnético $\vec{M}=\gamma \vec{S}$. En $t=0$ el estado del sistema es $\vert\psi(0) \rangle = \vert+ \rangle$. Dejamos evolucionar el sistema bajo la influencia de un campo magnético constante, paralelo al eje $y$, de módulo $B_0$. Calcular en la base $\{ \vert+ \rangle \, , \, \vert- \rangle \}$ el estado del sistema en un instante $t$. En dicho instante $t$ se miden $S_x$, $S_y$ y $S_z$; ¿qué valores se pueden obtener, y con qué probabilidades?

3. Una partícula de masa $m$, eléctricamente neutra y de spin $1/2$, está sometida a la acción de un campo magnético $\vec{B}(t)$. El hamiltoniano del sistema es $H=-\gamma \vec{\sigma} \cdot \vec{B}$, donde $\vec{\sigma}$ son las matrices de Pauli.

a) Escribir la ecuación de Schrödinger para la función de onda de spin $\kappa(t)$.

b) Si $\vert\kappa(t) \rangle = \lambda_1(t)\vert+ \rangle + \lambda_2(t)\vert- \rangle$, escribir las ecuaciones que satisfacen $\lambda_1(t)$ y $\lambda_2(t)$.

c) Sea $\vec{B}(t)$ paralelo al eje $z$, y $B(t)=B_0(1-e^{-\alpha t})$. Calcular $\lambda_1(t)$ y $\lambda_2(t)$ si $\lambda_1(0)=\cos \alpha_0$ y $\lambda_1(0)=\sin \alpha_0$ (con $0< \alpha_0 < \pi /2$).

4. Una partícula de spin $1/2$ y momento magnético $\gamma$ está sometida a un campo magnético en la dirección del eje $z$ de módulo $B_0$. Considérese el operador $\hat{A}$ definido por $\hat{A}=(1+\alpha \hat{S}_x)^2$, donde $\alpha \in \mathbb{C}$.

a) Supongamos que en $t=0$ el estado de la partícula es $\vert\psi (0) \rangle = \hat{A} \vert+ \rangle$. ¿Tiene $\vert\psi (0) \rangle$ un valor bien definido de $S_z$? ¿Es $\vert\psi (0) \rangle$ un estado estacionario?

b) ¿Qué condición se debe cumplir para que $\vert\psi (0) \rangle$ esté normalizado? ¿Cuáles son los valores posibles de una medida de la energía? ¿Cuál es la probabilidad de que una medida de la energía dé como resultado $E=-\gamma B_0 \hbar /2$?

c) Hallar los valores medios de $\hat{S}_x$ y $\hat{S}_y$ en el estado $\vert\psi \rangle$.

d) ¿Cómo evoluciona $\langle \hat{S}_z \rangle$ con el tiempo?

e) Calcular para qué valor de $t$ el sistema se encuentra en un estado cuya componente $S_y$ vale $\hbar/2$.

5. Un átomo de hidrógeno se halla en su estado fundamental. Aplicamos un campo magnético constante, de módulo $B_0$, paralelo al eje $x$. La energía de interacción electrón-campo magnético viene dada por:

$$H=-g_l\vec{L} \cdot \vec{B} -g_s\vec{B} \cdot \vec{S} \qquad ,$$

donde $g_l$ y $g_s$ son los factores giromagnéticos orbital y espinorial, respectivamente.

a) Pasado un tiempo $t_0$, ¿cuál es la probabilidad de encontrar el átomo en su primer estado excitado?

b) ¿Cuál debe ser el estado inicial de polarización del átomo para que dicha polarización no varíe al aplicar el campo magnético? Escribir dicho estado inicial en función de los autoestados de $S_z$ y $L_z$.

6. Una partícula sin spin en un potencial central se halla en el estado de energía más baja en el que la probabilidad de obtener el valor $2\hbar ^2$ al medir el momento angular total es 1. Se sabe, además, que $\langle L_z \rangle =0$.

Se somete la partícula a la acción de un campo magnético uniforme y constante en la dirección del eje $z$ y se deja evolucionar el sistema. Cuando $t=\pi / \mu B_0$ la probabilidad de encontrar la partícula en el mismo estado que en $t=0$ es 1.

a) Calcular el estado de la partícula en $t=0$ si $\langle L_+^2 \rangle (t=0) = -(1/2)\hbar ^2$.

b) Calcular la evolución temporal de $\langle L_z \rangle$,$\langle L_+ \rangle$, $\langle L_- \rangle$ y $\langle L_+^2 \rangle$.

7. Una partícula de spin $1/2$ tiene un momento magnético $\vec{M}=g\vec{S}$. En un instante $t=0$ el estado de dicha partícula está descrito por la función de onda:

$$\vert\psi \rangle = c_1 \vert+ \rangle + c_2 \vert- \rangle \qquad ,$$

con $c_1$ real y $c_2$ complejo, y $\vert \pm \rangle$ los autoestados de $S_z$. Los valores medios de $S_x$ y $S_y$ en ese estado son $\sqrt{3}\hbar /8$ y $3\hbar /8$, respectivamente.

a)Demostrar que $c_1=\sqrt{3}/2$ y $c_2=(1/2) \exp (i \pi /3)$.

b) Hallar los valores medios de $S_z$, $S_z^2$ y $S^2$.

c) Sometemos la partícula a la acción de un campo magnético uniforme $\vec{B}$ en la dirección $\vec{u}=(\theta=\pi /3 , \phi=\pi /3)$ y de módulo $B_0$, y la dejamos evolucionar. ¿Cuál será el estado de la partícula al cabo de un tiempo $t_0$?

d) Supóngase ahora que el campo magnético es paralelo a un eje perpendicular a $\vec{u}$. La probabilidad de encontrar $\hbar/2$ como resultado de una medida de la proyección de $\vec{S}$ a lo largo de $\vec{u}$ tiene, en ese caso, un comportamiento oscilante en el tiempo. Demostrarlo, y obtener el valor de la frecuencia de la oscilación.

8. Considérese el sistema formado por un quark y un antiquark. Ambas partículas tienen igual masa y spin $1/2$. Suponga que la interacción entre ellas está descrita por el potencial:

$$V(\vec{r_1} , \vec{r_2})=\frac{1}{2}m \omega^2 \vert(\vec{r_1} - \vec{r_2})\vert^2$$

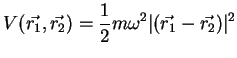
a) Construir un conjunto completo de observables que conmutan (CCOC) que incluya el hamiltoniano y $L_z$. Escribir las autofunciones del CCOC.

b) ¿Cuáles son los valores más bajos de la energía del sistema? ¿Qué degeneración tiene cada una de estas energías? Escribir todos los autoestados correspondientes a las mismas.

c) Sometemos el sistema a la acción de un campo magnético débil, constante y paralelo al eje $z$. Su intensidad es $B_0$. ¿Cómo se modifican las energías de los estados anteriores? ¿Y las funciones de onda?

d) Supóngase que el campo magnético es paralelo al eje $x$. ¿Cómo varía la energía del nivel más bajo? ¿Cuál será su función de onda?

e) Se vuelve a orientar el campo magnético en la dirección del eje $z$. ¿Cómo evolucionará en el tiempo el estado de energía más baja del apartado anterior?

9. Dos partículas de spin $1/2$, que tienen la misma masa pero no son idénticas, se hallan sometidas a la acción de un potencial:

$$V=\frac{1}{2}m \omega^2 x_1^2 + \frac{1}{2}m \omega^2 x_2^2$$

Además, interactúan entre sí mediante un potencial:

$$U=-\epsilon \vec{s}_1 \cdot \vec{s}_2$$

Obtener los autovalores y autovectores más bajos del sistema, suponiendo $\hbar \omega = 2\epsilon \hbar^2$. Si aplicamos un campo magnético paralelo al eje $z$ y de módulo $B_0$, ¿cómo variarán los autovalores y autovectores del sistema? ¿Y si el campo magnético es paralelo al eje $x$?

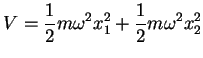
10. Una partícula de espín 1/2 y momento magnético $\vec{M}=g\vec{S}$ se encuentra en el estado

$\Psi = A \;\vert \frac{1}{2} \; +\frac{1}{2} > + \; B \;\vert \frac{1}{2} \; -\frac{1}{2} >$

siendo A y B tales que los valores esperados de $S_x$ y $S_y$ son iguales entre sí y a $\hbar \sqrt{3} /4 \sqrt{2}$.

a) Calcular A, B y el valor esperado de $S_z$

b) Se somete la partícula a la acción de un campo magnético uniforme $\vec{B_0}$ dirigido según el eje Y. Calcular el valor esperado de $S_z$ transcurrido un tiempo $t=\pi/g B_0$.

11. Dos partículas idénticas de espín 1/2 sólo pueden moverse en un plano, en el que además están confinadas por un potencial que es infinito en el exterior de un cuadrado de lado L y cero en su interior.

a) Escriba las funciones de onda del estado fundamental y del primer (o primeros) estados excitados del sistema.

b) De entre todos los estados excitados del apartado anterior, seleccione uno de parte espacial antisimétrica y de máxima proyección de espín sobre el eje Z. Imagine que hemos preparado el sistema en ese estado y que lo dejamos evolucionar sometido a un campo magnético constante ($B$) dirigido según el eje Y. Las partículas, que son neutras, tienen un momento magnético debido a su espín $\vec{M}= g \cdot \vec{S}$. Transcurrido un tiempo $t_0$, obtenga la funcion de ondas del estado y el valor esperado de la proyección del espín sobre el eje Z.

12. Dos electrones se encuentran atrapados en un potencial unidimensional que es cero en una región de longitud L e infinito fuera de ella. Los electrones se encuentran en un estado triplete de espín y en el estado del pozo de menor energía compatible con el requerimiento anterior.

a) Calcular su energía y escribir todas sus posibles funciones de onda.

b) Polarizamos el sistema de tal modo que la proyección del espín total de los electrones sobre el eje Z sea cero. A continuación aplicamos un campo magnético uniforme de intensidad B$_0$ dirigido según el eje Y. Calcular el valor esperado de la proyección sobre el eje Z del espín total como función del tiempo.

c) Repetir el apartado anterior si la proyección del espín total de los electrones sobre el eje Z es +1.

13. Dos electrones están confinados en una dimensión por un potencial infinito. Calcular sus dos autoenergías más bajas y todas las autofunciones correspondientes, explicitando para cada una de ellas el valor del espín total y de su tercera componente.

Aplicamos un campo magnético débil, de intensidad constante B$_0$, en la dirección del eje X. ¿Cómo se modificarán las autoenergías del sistema?

Preparamos el sistema en el estado S=1, S$_z$=0 y aplicamos un campo magnético constante B$_0$ en la dirección del eje X. ¿Cuánto valdrán los valores esperados de S$^2$ y S$_z$ como función del tiempo?

14. Dos partículas idénticas de espín 1/2 sólo pueden moverse en un plano, en el que además están confinadas por un potencial que es infinito en el exterior de un cuadrado de lado L y cero en su interior.

a) Escriba las funciones de onda del estado fundamental y del primer (o primeros) estados excitados del sistema.

b) Suponga el sistema en su estado fundamental. Lo dejamos evolucionar sometido a un campo magnético constante ($B$) dirigido según el eje Y. Las partículas, que son neutras, tienen un momento magnético debido a su espín $\vec{M}= g \cdot \vec{S}$. Transcurrido un tiempo $t_0$, obtenga la funcion de ondas del estado y el valor esperado de la proyección del espín sobre el eje Z.

15. Dos electrones se encuentran en un estado triplete cuya proyección del espín en la dirección del eje Z es S$_z$= 0. Aplicamos un campo magnético constante en la dirección de la bisectriz del primer cuadrante del plano XY.

a) Escribir la función de ondas de los electrones transcurrido un tiempo t.

b) Demostrar que el valor esperado de S$_x$ es cero para cualquier valor del tiempo.

16. Dos electrones están confinados en un pozo de potencial unidimensional infinito de anchura L.

a) Calcular sus dos autoenergías más bajas y todas las autofunciones correspondientes, explicitando para cada una de ellas el valor del espín total y de su tercera componente.

b) Imagine que, además, los electrones están sometidos a la acción de un campo magnético, de intensidad constante B$_0$, en la dirección de la bisectriz del primer cuadrante del plano XY. ¿Cuáles serán las nuevas autoenergías del sistema?

c) Desactivado el campo magnético del apartado b), preparamos el sistema en un estado S=1, S$_z$=0 y aplicamos otro campo magnético constante B$_1$ en la dirección del eje X. ¿Cuánto valdrán los valores esperados de S$^2$ y S$_z$ como función del tiempo?

17. Dos electrones se hallan confinados en un pozo de oscilador armónico unidimensional de frecuencia $\omega_0$. Se aplica un campo magnético constante. Obtener las cuatro autoenergías más bajas del sistema y escribir las autofunciones correspondientes.

18. Una partícula cuyo momento magnetico es $\vec{\mu}$ y cuyo espín vale 1/2, está polarizada en la direccion OX. Se aplica un campo magnético constante paralelo al eje OZ, $\vec{B_0}$. ¿Cuál será el valor esperado de S$_x$ como funcion del tiempo?

19. El quarkonio es un sistema ligado de un quark ($q$) y un antiquark ($\bar{q}$). Ambas son partículas de espín $s$=1/2 y tienen la misma masa (m$_q$). Supongamos que su interacción se puede describir mediante el potencial siguiente:

$$V = \displaystyle{\frac{1}{2}} m_q \omega^2 (\vec{r_q} - \vec{r_{\bar{q}}})^2$$

Sometemos al quarkonio a la acción de un campo magnético constante y paralelo al eje 0Z, $\vec{B_0}$, lo que resulta en un nuevo término de interacción de la forma:

$$V_{mag} = \displaystyle{\frac{\mu_q}{\hbar}} (\vec{s_q} - \vec{s_{\bar{q}}}) \cdot \vec{B_0}$$

a) Escriba el conjunto completo de observables que conmutan adecuado para este sistema.

b) Obtenga los cuatro autovalores más bajos de la energía y sus correspondientes autovectores.

c) Añadimos otro campo magnético constante, $\vec{b_0}$, paralelo al eje OX y tal que $b_0 << B_0$, ¿Cómo de modificarán las energías de los estados del apartado b)?

20. Una partícula de carga $q$ esta confinada en el plano XY y sujeta a la acción de un potencial de oscilador armónico bidimensional e isótropo de frecuencia $\omega$. Aplicamos sendos campos eléctricos constantes y de igual módulo ($E$) en las direcciones OX y OY. Encontrar los autovalores de la energía de la partícula. Verificar (para el estado fundamental) que si tratáramos el efecto de los campos eléctricos en teoría de perturbaciones, recuperaríamos el resultado exacto a segundo orden. Sabría verificarlo para cualquier estado?

21. Dos electrones se encuentran atrapados en un potencial unidimensional que es infinito excepto en un segmento de longitud L. Construir la autofunciones correspondientes a los dos autovalores más bajos de la energía, especificando los valores de los números cuánticos relevantes. Si aplicaramos un campo magnético $\vec{B_0}$, constante, en la dirección del eje OX, cómo variarían las autoenergías de los electrones?, cuáles serían sus nuevas autofunciones?

22. El positronio es el sistema ligado de un electrón y su antipartícula, el positrón. Ambas tienen la misma masa y sus cargas y momentos magnéticos tienen signo opuesto.

$$\vec{M}_{e^-} = - \vec{M}_{e^+} = - \displaystyle{\frac{2}{\h... ...\;\; \mu_B = \displaystyle{\frac{\vert e\vert \hbar}{2 m_e c}}$$

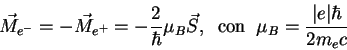
a) Calcule la energía de ligadura del positronio en su estado fundamental (1s), considerando unicamente la interaccción Coulombiana entre el electrón y el positrón. Escriba la (o las) funciones de ondas correspondientes a dicha autoenergía.

b) Obtenga las autoenergías de los estados (1s) cuando, además de la interacción Coulombiana, tenemos en cuenta la interacción hiperfina entre los momentos magnéticos:

$$H_1 = \beta \; \vec{M}_{e^-} \cdot \vec{M}_{e^+}$$

c) Repita el apartado b) si añadimos un campo magnético externo constante, dirigido segun el eje Z+, lo que resulta en un nuevo término en el hamiltoniano de la forma:

$$H_2 = - ( \vec{B_0} \cdot \vec{M}_{e^-} + \vec{B_0} \cdot \... ...\vert B_0\vert = \displaystyle{\frac{\sqrt{5}}{2}} \beta \mu_B$$

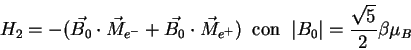
23. La función de ondas de dos partículas idénticas de espín 1/2 viene dada por:

$\Phi(x_1,x_2)= \displaystyle{ \frac{\sqrt{2}}{L} ( sen\frac{\pi x_1}{L} \cdot... ... sen\frac{\pi x_2}{L})} ( \vert 1/2 \: -1/2 >_1 \cdot \vert 1/2 \: -1/2 >_2 )$

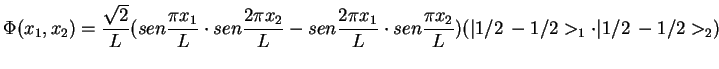
y es autoestado de un hamiltoniano que no contiene términos dependientes del espín.

a) Escriba el hamiltoniano y la autoenergía del estado.

b) Describa y justifique la forma del autoestado y obtenga el valor de su espín.

c) A partir de la autofunción dada, obtenga otra con la misma energía y cuyo espín difiera del suyo en una unidad de $\hbar$.

d) Cuáles serían las autoenergías más bajas del sistema si añadiéramos al hamiltoniano un término $h^{\prime} = \alpha (S_{x} + S_{y}$) ?