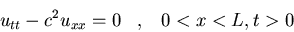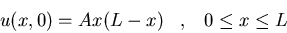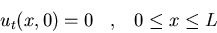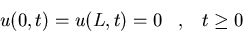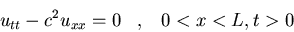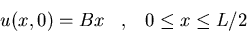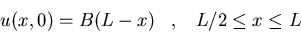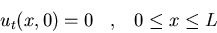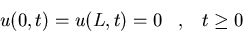Next: About this document ...
METODOS MATEMATICOS II (2do. PARCIAL)
Hoja I
- 1.
- Hallad la solución de las siguientes ecuaciones en derivadas
parciales:
- a)
- uxx=0
- b)
-
uxx+u=0
- c)
-
uxy+x2 uy =0
- d)
-
uxy+ux=0
- e)
-
uxy=sen(x) + ey
En todos los casos u es una función de dos variables
independientes, u=u(x,y).
- 2.
- Verificad que las funciones
u1(x,y)=x2-y2 y
u2(x,y)=ex sen(y)
son soluciones de la EDP
uxx+uyy=0.
- 3.
- Demostrad que si
u(x,y)=f(xy) donde f es una función
derivable arbitraria, entonces u satisface la EDP
x ux - y uy = 0.
- 4.
- Hallad la solución general de la EDP
uxx-4 uxy + 3 uyy=0
suponiendo que la solución es de la forma
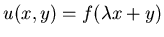 donde
donde 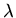 es un parámetro desconocido.
es un parámetro desconocido.
- 5.
- Determinad la región en que cada ecuación es hiperbólica,
parabólica o elíptica. Asimismo, en cada región, hallad la
forma canónica de la EDP:
- a)
-
xuxx+uyy=x2
- b)
-
uxx+y2 uyy=y
- c)
-
uxx+x y uyy=0
- d)
-
x2 uxx -2 x y uxy + y2 uyy = ex
- e)
-
uxx+uxy-x uyy = 0
- f)
-
ex uxx + ey uyy =u
- g)
-
sen2(x) uxx + sen(2x) uxy + cos2(x) uyy=x
- h)
-
uxx-y uxy +x ux +y uy + u =0
- 6.
- Obtened la solución general de las siguientes EDP:
- a)
-
x2 uxx + 2xy uxy + y2 uyy +xy ux + y2 uy = 0
- b)
-
r utt -c2 r urr -2 c2 ur = 0 donde c es una
constante y u=u(r,t) (sugerencia: haced el cambio v=r u).
Comprobad las soluciones por sustitución.
- 7.
- Reducid las siguientes EDP a su forma canónica y encontrad las
curvas características:
- a)
-
uxx+2uxy+3uyy+4ux+5uy+u=ex
- b)
-
2uxx-4uxy+2uyy+3u=0
- c)
-
uxx+5uxy+4uyy+7uy=sen(x)
- d)
-
uxx+uyy+2ux+8uy+u=0
- e)
-
uxy+2uyy+9ux+uy=2
- f)
-
6uxx-uxy+u=y2
- g)
-
uxy+ux+uy=3x
- h)
-
uyy-9ux+7uy=cos(y)
- 8.
- Hallad la solución general de las siguientes EDP:
- a)
-
uxx+uyy=0
- b)
-
uxxxx+2uxxyy+uyyyy=0 (sugerencia: usad z=x+iy).
- c)
-
uxx-3uxy+2uyy=0
- d)
-
uxx+10uxy+9uyy=y
- 9.
- Determinad la solución de los siguientes problemas con
condiciones iniciales para la cuerda infinitamente larga:
- a)
-
utt-c2 uxx = 0, u(x,0)=0,
ut(x,0)=1;
- b)
-
utt-c2 uxx = 0,
u(x,0)=sen(x),
ut(x,0)=x2;
- c)
-
utt-c2 uxx = 0,
u(x,0)=x3,
ut(x,0)=x;
- d)
-
utt-c2 uxx = 0,
u(x,0)=log(1+x2),
ut(x,0)=2;
donde u=u(x,t), c es una constante y los rangos son
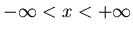 ,
,
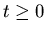 .
.
- 10.
- Resolved el problema:
uxx + 2 uxy -3 uyy=0
en
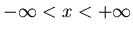 ,
,
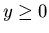 ,
con las condiciones:
,
con las condiciones:
- 11.
- Determinad la solución de cada uno de los siguientes
problemas donde u=u(x,t),
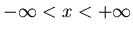 ,
,
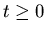 :
:
- a)
-
utt-c2 uxx=x, u(x,0)=0,
ut(x,0)=3.
- b)
-
utt-c2 uxx=x+ct, u(x,0)=x,
ut(x,0)=sen(x).
- c)
-
utt-c2 uxx=ex, u(x,0)=5,
ut(x,0)=x2.
- d)
-
utt-c2 uxx=xet,
u(x,0)=sen(x),
ut(x,0)=0.
- 12.
- Hallad la solución de los siguientes problemas con condiciones
iniciales y de contorno:
- a)
- Calculad
u(x,t=L/c) donde u(x,t) satisface:
donde A es una constante.
- b)
- Calculad
u(x,t=L/c) donde u(x,t) satisface:
donde B es una constante.
- 13.
- Un gas se encuentra en reposo inicialmente y contenido dentro
de una esfera de radio R. La condensación inicial está
dada por s0 dentro de la esfera y cero fuera. La condensación
está relacionada con el potencial de velocidades mediante
y el potencial de velocidades satisface la ecuación
utt= uxx + uyy + uzz.
Determinad la condensación s para todo t>0.
- 14.
- Dado el problema:
- a)
- Hallad
u(1/2,3/2) si L=c=1, f(x)=0,
g(x)=x(1-x).
- b)
- Hallad u(3/4,2) si L=c=1,
f(x)=x(1-x),
g(x)=x2(1-x).
- 15.
- Demostrad que la solución general del problema anterior verifica:
- a)
- es una función periódica impar en la variable x con
período 2L;
- b)
- es una función periódica con período 2L/c en la
variable t;
- c)
-
u(L-x,t+L/c)=-u(x,t).
- 16.
- Hallad la solución del problema:
- 17.
- Obtened la solución del problema:
- 18.
- Hallad u(x,t) que satisface:
- 19.
- Resolved el problema:
- 20.
- Demostrad que si u satisface la ecuación de ondas
unidimensional y
ux(0,t)=ux(L,t) para todo
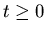 ,
entonces se satisfacen las siguientes relaciones
de recurrencia:
,
entonces se satisfacen las siguientes relaciones
de recurrencia:
- 21.
- Hallad la solución de:



Next: About this document ...
Gustavo Yepes Alonso
1998-03-13