- a)
- b)
- c)
- d)
3.
- a)
- b)
- c)
4.
- a)
- b)
- c)
5.
- a)
- b)
- c)
donde
f(1)=0 y f está acotada cuando ![]() .
.
donde
f(0)=0 y f está acotada cuando ![]() .
.
donde
f(1)=0, f está acotada cuando ![]() y n está fijado ( n=0,1,2,3,...).
y n está fijado ( n=0,1,2,3,...).
donde
f está acotada cuando ![]() .
Demostrad que sus autofunciones son los polinomios de Legendre (Pn(x))
y los autovalores correspondientes
.
Demostrad que sus autofunciones son los polinomios de Legendre (Pn(x))
y los autovalores correspondientes ![]() .
.
- a)
-
Desarrollad
la función g(x)=sen(x),
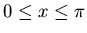 ,
en términos de las autofunciones del sistema de Sturm-Liouville
,
en términos de las autofunciones del sistema de Sturm-Liouville - b)
-
Desarrollad
la función g(x)=x,
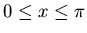 ,
en términos de las autofunciones del sistema de Sturm-Liouville
,
en términos de las autofunciones del sistema de Sturm-Liouville - c)
-
Desarrollad
la función g(x)=x(x-2),
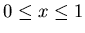 ,
en términos de las autofunciones del sistema de Sturm-Liouville
,
en términos de las autofunciones del sistema de Sturm-Liouville
- a)
- b)
- c)
- a)
- b)
- a)
- b)
donde
f(1)=0 y f está acotada cuando ![]() .
.
donde
f está acotada cuando ![]() .
.
- a)
- b)
- c)
donde f(0)=f(1)=0.
donde ![]() .
.
donde f(0)=f(1)=0.
donde ![]() satisface las siguientes condiciones: f es continua en
satisface las siguientes condiciones: f es continua en ![]() ,
, ![]() y
y ![]() es continua a trozos. (NOTA: úsese el principio del máximo
y del mínimo como ayuda en la demostración).
es continua a trozos. (NOTA: úsese el principio del máximo
y del mínimo como ayuda en la demostración).
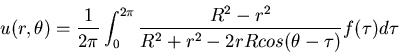
es
solución del problema anterior. Asimismo, demostrad a partir de
ésta fórmula que el valor de u en el origen (centro
del círculo) es igual al promedio de u sobre la circunferencia
(el llamado teorema del valor medio).
donde
u está acotada cuando ![]() .
Expresad la solución de la forma:
.
Expresad la solución de la forma:
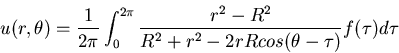
Nótese
que se diferencia de la fórmula de Poisson para el problema ``interior''
solamente en un cambio de signo.
donde ![]() satisface la condición
satisface la condición
Aplicad el método de separación de variables y expresad el resultado de la forma:
donde
C es una constante indeterminada.
donde D es un dominio conexo y acotado, y
(es
decir, que la integral de línea de f a lo largo de la frontera
F se anula).
- a)
- b)
- c)
y ![]() está acotada. La constante
está acotada. La constante ![]() toma un valor entre 0 y
toma un valor entre 0 y ![]() .
.
descomponiendo
u=v+w de manera que w satisface la ecuación
inhomogénea ( ![]() )
y resolved la ecuación en w suponiendo que w es un
polinomio.
)
y resolved la ecuación en w suponiendo que w es un
polinomio.
donde se satisface la condición de compatibilidad