-
1.
-
Hallad la función de Green en
cada uno de los siguientes problemas y usadla para expresar la solución
en términos de la función F dada en cada caso:
-
a)
-
Círculo de radio R:
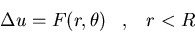
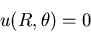
-
b)
-
Círculo de radio R:
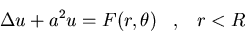
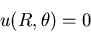
donde a es una constante.
-
c)
-
Bola de radio R:
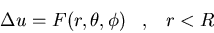
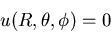
-
d)
-
Bola de radio R:
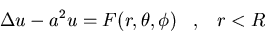
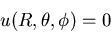
donde a es una constante.
-
e)
-
Paralelepípedo:
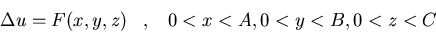 u(0,y,z)=u(A,y,z)=u(x,0,z)=u(x,B,z)=u(x,y,0)=u(x,y,C)=0
u(0,y,z)=u(A,y,z)=u(x,0,z)=u(x,B,z)=u(x,y,0)=u(x,y,C)=0
-
2.
-
Resolved los siguientes problemas mediante
la función de Green:
-
a)
-
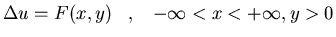
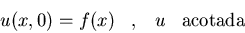
-
b)
-
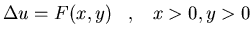
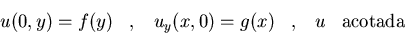
-
c)
-
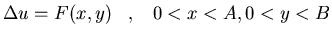
u(0,y)=u(A,y)=u(x,0)=u(x,B)=0
-
3.
-
Resolved el siguiente problema (en
el exterior del círculo unidad) usando la función de Green:
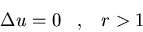
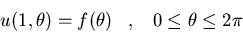
y u una función acotada.
-
4.
-
Hállese la función de
Green que satisface:
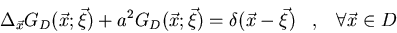
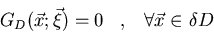
donde el dominio D está
dado por
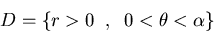
con 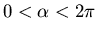 y
y 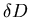 es la frontera de dicho dominio D.
es la frontera de dicho dominio D.
-
5.
-
Resuélvase el siguiente problema
mediante el uso de la función de Green:
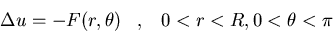
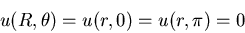
-
6.
-
Hallad la solución del siguiente
problema de Dirichlet usando la función de Green:
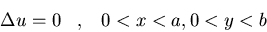
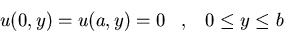
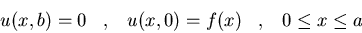
-
7.
-
Hallad la función de Green para
la región semi-infinita z>0 en el espacio tridimensional:
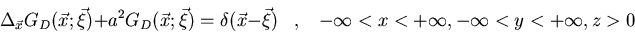
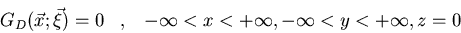
-
8.
-
Hállese la función de
Green para el cuadrante x>0, y>0 en el espacio bidimensional:
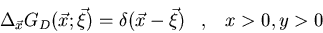
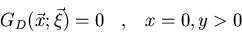
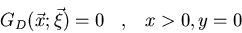
-
9.
-
Determinad la función de Green
que satisface:
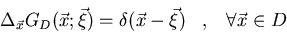
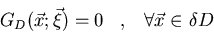
y GD acotada.
La región D es la banda semi-infinita 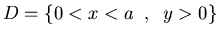 y
y 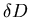 es la frontera de D.
es la frontera de D.
-
10.
-
Determinad la función de Green
que satisface:
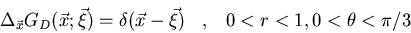
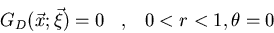
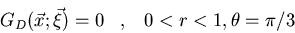
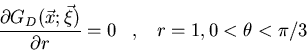
donde 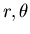 son las coordenadas polares de
son las coordenadas polares de 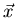 .
.
-
11.
-
Hallad la función de Green para
la ecuación
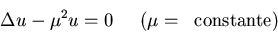
que se anula en todos los lados
del rectángulo 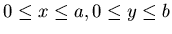 .
.
-
12.
-
Determinad la función de Green
para la ecuación de Helmholtz
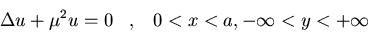
que se anula en los lados x=0
y x=a.
-
13.
-
Resolved el problema de Dirichlet para
el exterior de una esfera:
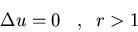
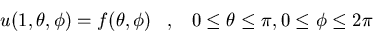
usando el método de la función
de Green. 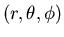 son las coordenadas esféricas de
son las coordenadas esféricas de 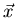 .
.
-
14.
-
Hallad la solución singular
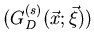 de la función de Green en 2 y 3 dimensiones para el operador
de la función de Green en 2 y 3 dimensiones para el operador 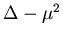 donde
donde 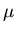 es una constante.
es una constante.
-
15.
-
Repetid el ejercicio anterior para
el operador
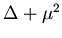 .
.
-
16.
-
Hallad la función de Green para
la ecuación de Helmholtz
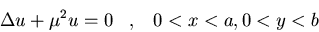
que se anula en los lados del rectángulo 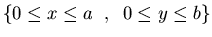 .
.
-
17.
-
Hallad la función de Green para
el operador de Klein-Gordon estático
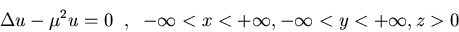
que se anula en el plano z=0.
-
18.
-
Demostrad que la función de
Green (en 2 dimensiones) para el operador de Klein-Gordon estático
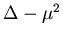 en la región
en la región 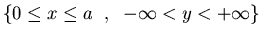 está dada por:
está dada por:
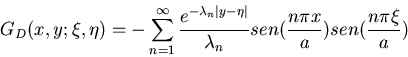
donde 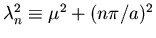 y se supone que
y se supone que 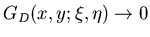 cuando
cuando 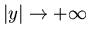 .
.
-
19.
-
Calculad el potencial ``electrostático''
en el espacio
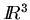 debido a dos cargas puntuales +q situada en (0,0,a/2) y -q
situada en (0,0,-a/2) cuando la
ecuación clásica de Poisson
debido a dos cargas puntuales +q situada en (0,0,a/2) y -q
situada en (0,0,-a/2) cuando la
ecuación clásica de Poisson 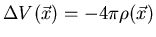 (donde
(donde 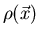 es la densidad de carga) se modifica de la siguiente manera:
es la densidad de carga) se modifica de la siguiente manera:
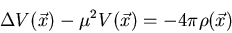
donde 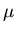 es una constante.
es una constante.
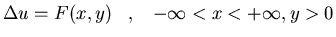
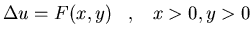
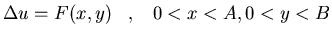
![]() y
y ![]() es la frontera de dicho dominio D.
es la frontera de dicho dominio D.
![]() y
y ![]() es la frontera de D.
es la frontera de D.
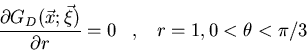
![]() son las coordenadas polares de
son las coordenadas polares de ![]() .
.
![]() .
.
![]() son las coordenadas esféricas de
son las coordenadas esféricas de ![]() .
.
![]() .
.
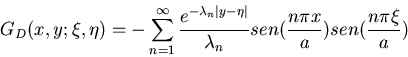
![]() y se supone que
y se supone que ![]() cuando
cuando ![]() .
.
![]() es una constante.
es una constante.