-
1.
-
Hallad la solución al siguiente
problema de Neumann en el semiplano y>0:
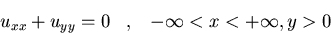
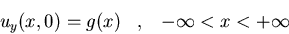
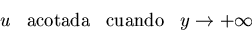
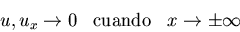
-
2.
-
Determinad la solución del problema:
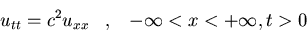

Es decir, hallad la solución
de D'Alembert usando la transformada Fourier.
-
3.
-
Resolved el siguiente problema:
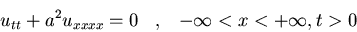

-
4.
-
Hallad la solución de los siguientes
problemas:
-
a)
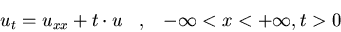
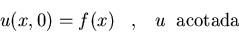
-
b)
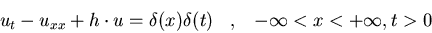
 u(x,0)=0
u(x,0)=0
-
5.
-
Hallad la solución del problema
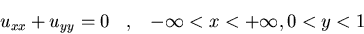
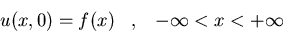
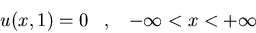
donde 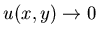 uniformemente en y cuando
uniformemente en y cuando 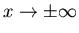 .
Asimismo hallad la solución en el caso particular en que f(x)=e-2|x|.
.
Asimismo hallad la solución en el caso particular en que f(x)=e-2|x|.
-
6.
-
Resolved el problema anterior mediante
el método de separación de variables con un desarrollo en
serie.
-
7.
-
Hallad la solución del siguiente
problema:
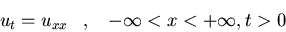
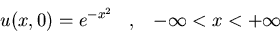
donde u es acotada.
-
8.
-
Resolved los siguientes problemas:
-
a)
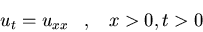
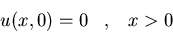
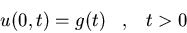
donde u es acotada. Asimismo,
hallad la solución en el caso particular en que g(t)=t
e-t.
-
b)
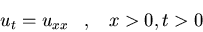
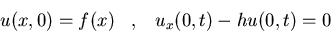
donde h es una constante
positiva.
-
c)
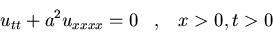
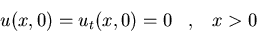
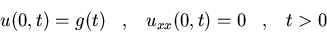
-
d)
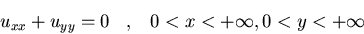
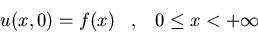
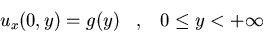
-
9.
-
Hallad la solución del problema:
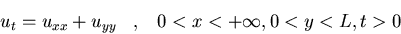 u(x,y,0)=u(0,y,t)=u(x,0,t)=0
u(x,L,t)=1
u(x,y,0)=u(0,y,t)=u(x,0,t)=0
u(x,L,t)=1
-
10.
-
Hallad la solución del siguiente
problema:
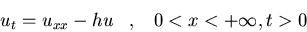
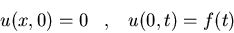
donde h es una constante
positiva.
-
11.
-
Resolved el siguiente problema:
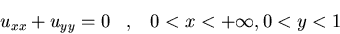
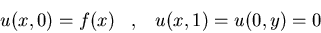
donde 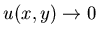 uniformemente en y cuando
uniformemente en y cuando 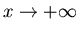 .
Asimismo, obtened la solución en el caso particular f(x)=e-x.
.
Asimismo, obtened la solución en el caso particular f(x)=e-x.
-
12.
-
Resolved el problema:
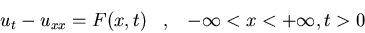 u(x,0)=0
u(x,0)=0
donde u es acotada.
-
13.
-
Demostrad que si u satisface
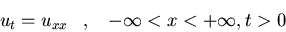
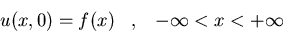
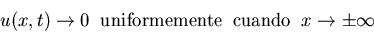
entonces se verifica que
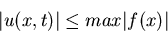
Sugerencia: aplicad el principio
del máximo y del mínimo para la ecuación del calor
a la banda 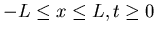 y haced
y haced 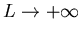 .
.
-
14.
-
Resolved el problema:
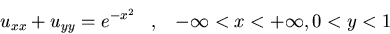 u(x,0)=u(x,1)=0
u(x,0)=u(x,1)=0
y 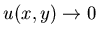 uniformemente en y cuando
uniformemente en y cuando 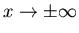 .
.
-
15.
-
Hallad la solución del siguiente
problema:
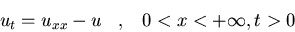
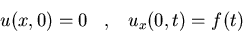
y u acotada. Expresad la
solución como una integral simple sobre f(t).
-
16.
-
Resolved el problema:
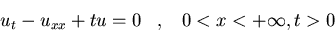
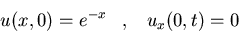
donde 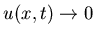 uniformemente en t cuando
uniformemente en t cuando 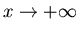 .
.
-
17.
-
Resolved el problema del flujo de calor
en 2 dimensiones:
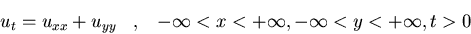
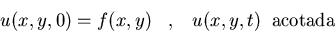
Asimismo, hallad la solución
en el caso particular en que f(x,y)=e-x2-y2.
-
18.
-
Resolved los siguientes problemas en
el espacio tridimensional:
-
a)
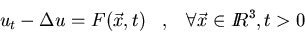
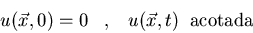
-
b)
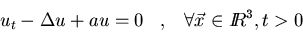
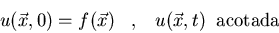
Asimismo, obtened la solución
en el caso particular en que 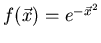 .
.
-
19.
-
Resolved el problema del movimiento
ondulatorio en 2 dimensiones:
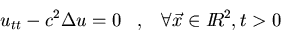
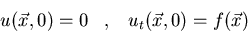
-
20.
-
Demostrad que si
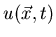 es la solución del problema
es la solución del problema
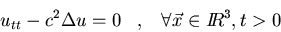
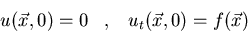
entonces 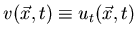 satisface la ecuación de ondas y las condiciones iniciales
satisface la ecuación de ondas y las condiciones iniciales 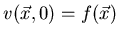 y
y 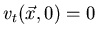 .
Partiendo de este resultado hallad la solución del problema de valores
iniciales:
.
Partiendo de este resultado hallad la solución del problema de valores
iniciales:
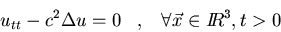

-
21.
-
Resolved el problema no homogéneo
siguiente en el espacio tridimensional:
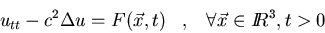
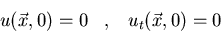
-
22.
-
Hallad
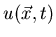 para el siguiente problema:
para el siguiente problema:
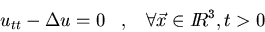
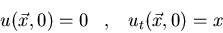
-
23.
-
Resolved el problema de la ecuación
del calor en 1 dimensión
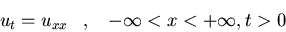
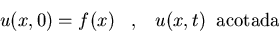
aplicando simultáneamente
la transformada Fourier y la transformada Laplace. Nota:
![\begin{displaymath}{\cal L}^{-1}[\frac{e^{-\sqrt{s}\vert x-y\vert}}{\sqrt{s}}] =\frac{1}{\sqrt{\pi t}} e^{-\frac{(x-y)^2}{4t}}\end{displaymath}](img67.gif)
-
24.
-
Resolved el siguiente problema mediante
la transformada de Laplace:
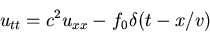 u(x,0)=ut(x,0)=u(0,t)=0
u(x,0)=ut(x,0)=u(0,t)=0
y u acotada cuando 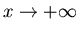 .
Considered el caso
.
Considered el caso 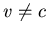 y el caso v=c.
y el caso v=c.
-
25.
-
Hallad las soluciones de los siguientes
problemas haciendo uso de la transformada Laplace:
-
a)
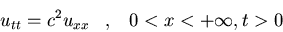
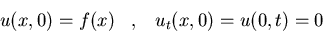
y 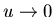 cuando
cuando 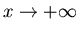 .
.
-
b)
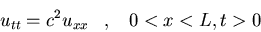 u(x,0)=ut(x,0)=0
u(x,0)=ut(x,0)=0
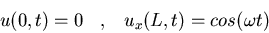
-
c)
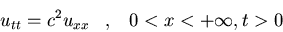 u(x,0)=ut(x,0)=0
u(x,0)=ut(x,0)=0
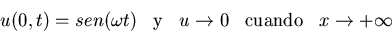
-
d)
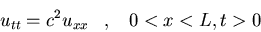 u(x,0)=ut(x,0)=0
u(x,0)=ut(x,0)=0
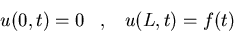
-
e)
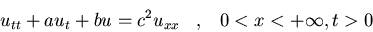 u(x,0)=ut(x,0)=0
u(x,0)=ut(x,0)=0
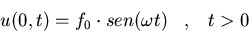
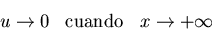
-
26.
-
Resolved los siguientes problemas haciendo
uso de la transformada Laplace:
-
a)
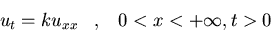
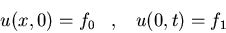
y 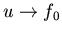 cuando
cuando 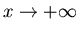 .
.
-
b)
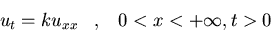
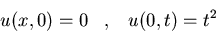
y 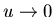 cuando
cuando 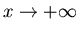 .
.
-
c)
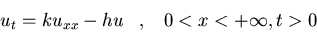
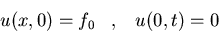
y 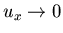 cuando
cuando 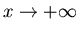 .
.
-
d)
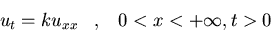

y 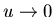 cuando
cuando 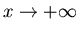 .
.
-
27.
-
Resolved el problema del sonido en
un rincón:
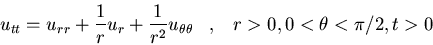
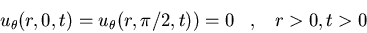
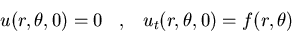
-
28.
-
Hallad la solución al siguiente
problema expresándola como una integral finita deformando el contorno
al calcular la transformada inversa de Laplace:
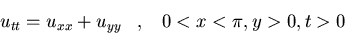 u(x,y,0)=ut(x,y,0)=0
u(x,y,0)=ut(x,y,0)=0
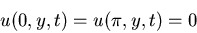 uy(x,0,t)+2
u(x,0,t)=sen(x)
uy(x,0,t)+2
u(x,0,t)=sen(x)
Nota: Aplíquese la
transformada de Laplace en la variable tiempo y úsese un desarrollo
en serie en la variable espacial x.
![]() uniformemente en y cuando
uniformemente en y cuando ![]() .
Asimismo hallad la solución en el caso particular en que f(x)=e-2|x|.
.
Asimismo hallad la solución en el caso particular en que f(x)=e-2|x|.
![]() uniformemente en y cuando
uniformemente en y cuando ![]() .
Asimismo, obtened la solución en el caso particular f(x)=e-x.
.
Asimismo, obtened la solución en el caso particular f(x)=e-x.
![]() y haced
y haced ![]() .
.
![]() uniformemente en y cuando
uniformemente en y cuando ![]() .
.
![]() uniformemente en t cuando
uniformemente en t cuando ![]() .
.
![]() .
.![]() satisface la ecuación de ondas y las condiciones iniciales
satisface la ecuación de ondas y las condiciones iniciales ![]() y
y ![]() .
Partiendo de este resultado hallad la solución del problema de valores
iniciales:
.
Partiendo de este resultado hallad la solución del problema de valores
iniciales:
![\begin{displaymath}{\cal L}^{-1}[\frac{e^{-\sqrt{s}\vert x-y\vert}}{\sqrt{s}}] =\frac{1}{\sqrt{\pi t}} e^{-\frac{(x-y)^2}{4t}}\end{displaymath}](img67.gif)
![]() .
Considered el caso
.
Considered el caso ![]() y el caso v=c.
y el caso v=c.
![]() cuando
cuando ![]() .
.
![]() cuando
cuando ![]() .
.
![]() cuando
cuando ![]() .
.
![]() cuando
cuando ![]() .
.
![]() cuando
cuando ![]() .
.